LCA
Updated:
서론 및 개인적인 생각
LCA는 최소 공통 조상을 뜻하며, 영어로는 Least Common Ancestor? 뭐 이런 의미 인거 같다
그럼 반대로 최대 공통 조상이란 말이 있을까라는 생각이 든다. 그런데, 사실 최대 공통조상의 정답은 너무 간단하다. 왜냐하면 항상 루트일것이기 때문이다
그러면 LCA를 통해서 무엇을 할수 있을것인가? 라는 고민이 문득 든다
이런 문제의 경우에 아주 적합할 것 같다
문제부터 대놓고 LCA 2이지만,
이 문제는 트리의 형태로 주어졌을때, 입력되는 쿼리에 대해서 최소 공통 조상을 빠르게 찾아야 한다는 문제이다
뭐 사실, 최소 공통조상이 아니고, 그냥 입력되는 쿼리의 사이의 거리를 구한다는 이런 유형의 문제가
거의 LCA관련 문제라고 생각한다(단, 입력되는 쿼리수가 많고, 구성하고 있는 트리의 노드 갯수도 많아야한다는 가정)
우리가 LCA를 모른다면, 일반적으로 생각하기에
매번 입력받는 쿼리마다 DFS혹은 BFS를 돌려서, 최소 공통 조상을 찾게된다
즉 그러면 시간복잡도는 대략, V: 노드 갯수, E:엣지 갯수, Q:쿼리 갯수라고 가정하면
O(Q(V+E)) 라는 시간 복잡도가 나올것이며, Q가 10000개만 넘어간다고 해도, 시간이 정말 많이 걸릴것이다
그래서, 이런 문제를 빠르게 해결하기 위해서 LCA를 통해 해결할수 있는데,
LCA 시간복잡도는 우선 좀있다가 보기로 하고,
LCA를 한번 구해야 한다. 근데, LCA가 어려울수 있는점이 LCA를 하기전에 2가지 Step이 필요하다!!
- dp[i][j]의 정의를 명확히 세우고 알아야 하는점
- DFS or BFS를 돌려서 바로 자신의 부모의 정보를 갱신해야 한다는점이다
이 2가지를 한다음에, 마지막에 LCA를 구한다면 올바르게 구할수 있음을 알수 있다
우선 dp[i][j]의 정의를 세워야 한다
Dynamic Programming의 수준까지는 아니지만, 뭔가 DP의 성질이 조금 반영은 되는데,
저 정의를 세우기 전에 이런 생각을 하게 된다
(어떻게 해야 목표 노드까지 빠르게 도달을 하지? -> 일일이 DFS or BFS를 돌릴순 없어 -> LCA를 대충 읽어보니 최소 공통조상 어쩌고 저쩌고네 -> 그러면 해당 i번째 노드에서 j번째위에 있는 조상이라고 정의하면 뭔가 그럴싸하지 않을까?)
이런 생각이 든다. 처음 배울때는 그런 생각이 들었다. 그런데, 저런 식의 정의를 세우면 , j가 10만일경우
dp[10만][10만] 이런 말도 안되는 경우가 나오게 된다(애초에 배열 선언도 안될지도 모름, 사실 안해봤음)
그러면 어떻게 해야 내 위에 있는 모든 조상들로 올바르게 접근을 할수 있을것인가 ? 라는 생각이 든다
이거는 컴퓨터의 성질인 2진수에 따른다고 생각을 한다(그냥 제 생각)
그렇다면 검증을 해봐야 한다
시작
dp[i][j]: i번째 노드의 2^j(2의 j승)번째 조상의 노드 번호 라고 정의를 해본다
그러면 i번째 노드의 50번째 조상을 찾는다고 생각을 해본다
그러면 50이란 숫자는 50=32+16+2 로 표현이 될것이다
즉, 32번째 조상으로 올라간다음, 그위치에서 다시 16번째 조상으로 올라간다음, 2번째 조상으로 올라가게 된다면
우리는 올바르게 i번째 위로 있는 모든 조상들을 올바르게 찾아낼 수 있을것이다
그러면 이제 이 작업을 하기 위해서
먼저 DFS 혹은 BFS를 통해, 바로 윗 부모가 누구인지 파악을 해주는 작업이 필요하다
DFS혹은 BFS를 돌리면서, 현재 위치의 노드와 바로 전 위치의 노드를 같이 가지고 간다면,
바로 윗부모의 정보를 올바르게 갱신시킬수 있을것이다
그리고 여기서 빠뜨린게 있는데, 해당 노드가 깊이가 얼마인지를 파악하는것이 중요하다
이것은 좀있다가 아래서 설명을 하도록 하겠다
DFS
void dfs(int here, int parent, int depth) {
visited[here] = true;
d[here] = depth; // 본인의 위치정보 갱신
par[here][0] = parent; // 바로 윗부모(2^0은 1이므로, 바로 윗부모를 알수 있다)
for (int i = 0; i < a[here].size(); i++) {
int next = a[here][i];
if (!visited[next]) {
dfs(next, here, depth + 1); // 현재정점과, 부모정점을 같이 전달을 한다
}
}
}
(시간복잡도는 O(V+E)이다) 위와 같이 한다면, 올바르게 바로 윗부모의 상태를 갱신시킬수 있을것이다 그러면 이제 2번째 단계는 dp[i][j]의 공간을 전부다 채워야 하는데, 그림을 그려보면 유추를 해볼수 있다
DP
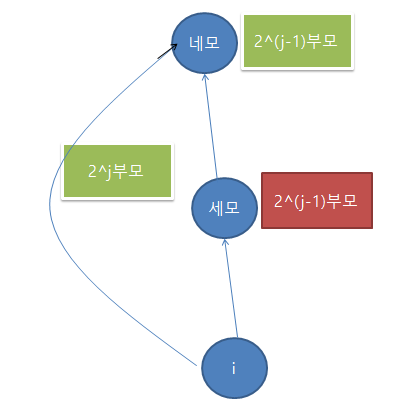
여기서 세모는 dp[i][j-1]일것이고, 네모는 dp[세모][j-1]일것이다
그때 dp[i][j]는 네모와 똑같은데, dp[세모][j-1]의 정보를 알고있다면
dp[i][j]에 dp[세모][j-1]을 넘기면서 전달을 해주는 것이다
그러면 dp[i][j]=dp[dp[i][j-1]][j-1] 이라는 수식이 나올것이다
이 과정을 통해 2단계를 할수 있다
void make() { //요거잘하기
for (int j = 1; j <= 17; j++) { //순서가 바뀌면 안됨!
for (int i = 1; i <= n; i++) {
par[i][j] = par[par[i][j - 1]][j - 1];
}
}
}
여기서 주의 할 사항은 위에 주석에도 있지만, 저 i랑 j의 순서가 절대 바뀌면 안된다
왜냐하면, 그냥 정점 하나에 대해서 갱신을 하게 될때는, 위에서 언급한 네모와 세모값이 올바르게 존재해야 par[i][j]에 올바르게 값을 대입시킬수 있는데, 순서를 바꿔서 갱신을 하게 되면, 세모의 2^(j-1)조상이 네모라는 정보가 없기 때문에, 갱신이 되지 않게 된다
세모의 조상이 네모라는 정보가 왜 없게되냐면, 지금 현재는 i번째 정점을 기준으로 위로 계속 갱신을 시키기 때문이다
그러므로 저 순서를 바꾸지 않아야 한다는걸 주의해야 한다, 시간복잡도는 O(i*j)일것이다
이렇게 2가지 과정이 완료되면, LCA를 하면 된다.
LCA
LCA의 동작원리는 다음과 같다
-
노드 A와 노드 B의 깊이가 다를때, 맞추려고 노력을 한다
-
그렇게 1의 과정을 열심히 해서 높이를 맞췄을때, 노드 A와 노드 B가 같다면, 더이상 올라갈 필요가 없기때문에 둘중 하나를 리턴해준다
-
높이는 맞췄는데, 조상이 다르다면, 반복문을 돌리면서 2^j번째 조상이 다를때마다, 그 조상의 위치로 계속 올린다
-
3번의 과정 후에 바로 직전위의 조상이 최소 공통조상이 된다
어차피 최소 공통조상을 찾으려면, 무조건 A와 B의 높이가 같아야 한다는 생각에 이르게 되기 때문에, 이걸 끼워맞추기(?) 위해서라도
높이를 일치시켜야 된다는 점이다. 그래서 아까 구해놓은 d배열(깊이배열)이 여기에 쓰이게 되는 것이다
코드를 보면 이해가 좀 더 빠를것 같다
int lca(int a, int b) {
// 깊이가 맞는지부터 확인,근데 보통 같지 않고, 같아도 어차피 걔바로위가 공통조상일지 모름 ㅇㅇ
if (d[a] > d[b]) swap(a, b); //우선 a보다 b가 무조건 깊이가 깊다고 몰빵 ㄱ
//b의 depth를 끌어올리기
for (int i = 17; i >= 0; i--) {
if (d[b] - d[a] >= (1 << i)) {
b = par[b][i];
}
}
if (a == b) return a; // 깊이는 같은데, 만약에 그냥 같아버리면 더이상 올라갈 필요 없으니 ㄱ
for (int i = 17; i >= 0; i--) { //깊이를 음, 바로직전까지만 올리자, 즉 부모가 다를때만 올리자 계속
if (par[a][i] != par[b][i]) {
a = par[a][i];
b = par[b][i];
}
}
return par[a][0];
}
아까 위의 설명처럼 깊이가 50이 차이가 난다면, 32+16+2일것이기 때문에, 높이가 큰수부터 깎는다고 생각을 하면 편할것 같다
50-32 -> 18-16-> 2인데, 2에서 2를 빼면 같은 조상이므로, 2-2->0까지 이렇게 만들면 된다
만약 높이가 같은데, 조상이 같지가 않았다면, 조상이 다를때 올려주면 된다
그게 무슨말이냐면, 큰수부터 조상을 봤는데 일치한다면 어차피 최소 공통조상을 찾을 수 없다. 일치해서 올리게 된다면, 그냥 최소 공통조상이 아니라 최대 공통 조상을 찾게되기 때문이다
그래서 다를때까지만 계속 올리면 맨마지막에는 바로 최소 공통조상 자식(A와 B)의 상태로 올것이기 때문에
그때의 바로 윗부모를 반환하면 된다
LCA 소스코드는 다음과 같다
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <queue>
#include <map>
#include <iostream>
#include <string>
#include <math.h>
#include <set>
#include <list>
#include <climits>
#include <string.h>
#include <deque>
#include <functional>
#include <stack>
using namespace std;
typedef long long ll;
#define INF 1000000000
typedef pair<int, ll> P;
typedef pair<pair<int, int>, int> PP;
typedef pair<int, pair<int, int>> PPP;
int gox[4] = { 0,1,-1,0 };
int goy[4] = { 1,0,0,-1 };
int n, m;
vector<vector<int>> a;
int par[100005][18];
int d[100005];
bool visited[100005];
void make() { //요거잘하기
for (int j = 1; j <= 17; j++) { //순서가 바뀌면 안됨!
for (int i = 1; i <= n; i++) {
par[i][j] = par[par[i][j - 1]][j - 1];
}
}
}
void dfs(int here, int parent, int depth) {
visited[here] = true;
d[here] = depth; // 본인의 위치정보 갱신
par[here][0] = parent; // 바로 윗부모(2^0은 1이므로, 바로 윗부모를 알수 있다)
for (int i = 0; i < a[here].size(); i++) {
int next = a[here][i];
if (!visited[next]) {
dfs(next, here, depth + 1); // 현재정점과, 부모정점을 같이 전달을 한다
}
}
}
int lca(int a, int b) {
// 깊이가 맞는지부터 확인,근데 보통 같지 않고, 같아도 어차피 걔바로위가 공통조상일지 모름 ㅇㅇ
if (d[a] > d[b]) swap(a, b); //우선 a보다 b가 무조건 깊이가 깊다고 몰빵 ㄱ
//b의 depth를 끌어올리기
for (int i = 17; i >= 0; i--) {
if (d[b] - d[a] >= (1 << i)) {
b = par[b][i];
}
}
if (a == b) return a; // 깊이는 같은데, 만약에 그냥 같아버리면 더이상 올라갈 필요 없으니 ㄱ
for (int i = 17; i >= 0; i--) { //깊이를 음, 바로직전까지만 올리자, 즉 부모가 다를때만 올리자 계속
if (par[a][i] != par[b][i]) {
a = par[a][i];
b = par[b][i];
}
}
return par[a][0];
}
int main() {
scanf("%d", &n);
a.resize(n + 1);
for (int i = 1; i < n; i++) {
int first, second;
scanf("%d%d", &first, &second);
a[first].push_back(second);
a[second].push_back(first);
}
dfs(1, 0, 0);
make();
scanf("%d", &m);
for (int i = 1; i <= m; i++) {
int first, second;
scanf("%d%d", &first, &second);
printf("%d\n", lca(first, second));
}
return 0;
}
출처: https://jason9319.tistory.com/90
이곳에서 공부를 많이 했습니다. 항상 좋은 글 감사드립니다
궁금하신 사항이 있으시면 댓글을 달아주시면 감사하겠습니다^^
잘못 된점 이 있다면 댓글 남겨주시면 감사드리겠습니다

Leave a comment