CCW교차판별
Updated:
이번의 경우는 CCW를 통해서 교차 판별을 이루는 문제를 파악해보려 합니다
CCW를 하면 반시계방향인지, 시계 방향인지를 알수 있습니다.
그러면 교차를 하려면 어떻게 형성이 되어야 할까요?
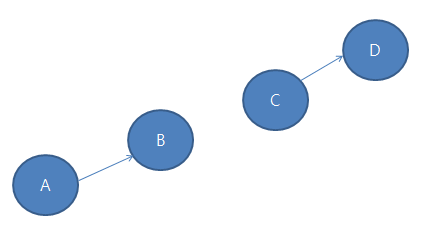
당연히 아래 그림과 같이 형성을 해야 할것입니다
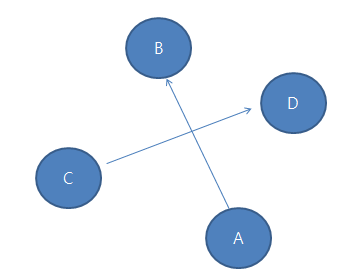
그러면 점 A와 B 그리고 C를 CCW한 값을 CCW1이라고 가정을 해보겠습니다
그때 CCW1의 값은 무조건 반시계방향이니까 양수일것입니다
그러면 한번더 점 A와 B, 그리고 점 D를 CCW한 값을 CCW2라고 가정을 해보겠습니다
그러면 CCW2는 시계방향이니까 음수 일것입니다.
그렇다면 CCW1*CCW2를 곱한 값이 음수면 되겠구나라고 생각을 할것입니다.
하지만 다음과 같은 반례가 있을수 있습니다.
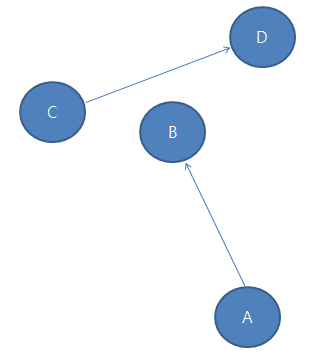
이와 같은 경우에는 CCW1*CCW2값이 음수겠지만, 교차는 하지 않습니다
그러면 CCW3을 점 C와 D 그리고 점 A를 CCW한 값
CCW4을 점 C와 D 그리고 점 B를 CCW한 값이라고 할때
이 두 값또한 음수가되어야 한다는 점을 이용하면 될것입니다
그러므로 교차 판별의 조건은 CCW1CCW2<0 && CCW3CCW4<0 이라는 조건을 통해 알 수 있습니다
근데 여기서 주의 해야 할것이, 이거는 문제마다 조금 잘 읽고 판단을 해봐야 한다고 생각을 하는데,
그냥 직선1이 직선2에 접한다. 즉 교점을 가지는데 위의 사진의 경우처럼 직선이 직선을 통과 하는 경우가 아니라, 90도 각도를 이루는 경우가 있습니다.
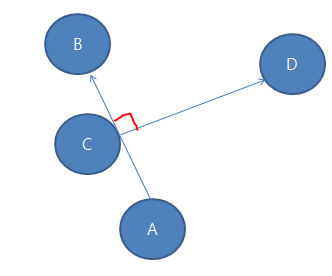
이런 경우는 CCW1한값이 (점 A,B,C) 일직선이기때문에 0이 나올것입니다
그래서 문제를 읽었는데 접하는 것도 직선이 만나는 것이다 라고 되어있다면, 저 위의 식을 조금 수정을 해야만 합니다
CCW1CCW2<=0 && CCW3CCW4<=0 이때의 경우만 된다는 것을 알수 있겠죠
근데 여기서도 예외처리를 해줘야 하는 경우가 있습니다
만약 CCW1CCW2==0 이고 그리고 CCW3CCW4==0 일때를 보면
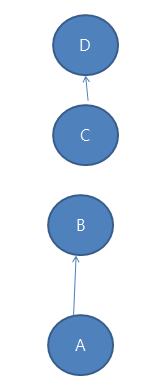
- x좌표가 전부 동일한 경우,그런데 y좌표가 접하지 않는경우
- 기울기가 동일한 경우(y좌표가 전부 다 같은 경우도 포함이 됨)
이러한 경우의 예외처리를 해줘야 한다
그러면, 이와 같이 코딩을 해주면 간단할 것이다
1. 맨먼저 x좌표가 다 똑같은 경우
- (a). 선분P의 최대 y좌표값과, 선분Q의 최소 y좌표값이 만나는지 안만나는지 check
- (b). 선분P의 최소 y좌표값과, 선분Q의 최대 y좌표값이 만나는지 안만나는지 check
2. 기울기가 동일한 경우
위와 마찬가지로 x좌표에 대해서 check를 해주면 된다
bool check(P A, P B, P C, P D) {
int x1 = A.first, y1 = A.second, x2 = B.first, y2 = B.second, x3 = C.first, y3 = C.second, x4 = D.first, y4 = D.second;
if (x1 == x2 && x2 == x3 && x3 == x4 & x4 == x1) { //x좌표 겹칠때(y좌표비교)
int maxy = max(y1, y2);
int miny = min(y3, y4);
if (maxy < miny) return false;
int maxy2 = max(y3, y4);
int miny2 = min(y1, y2);
if (maxy2 < miny2) return false;
}
else { //그외 나머지(기울기가 동일하다거나, y좌표가 겹친다거나)
int maxx = max(x1, x2);
int minx = min(x3, x4);
if (maxx < minx) return false;
int maxx2 = max(x3, x4);
int minx2 = min(x1, x2);
if (maxx2 < minx2) return false;
}
return true;
}
위에 써놓은 말을 그대로 코드로 풀어썼다. 코드가 좀 길어서 난잡할수는 있습니당 ㅠㅠ
그리고 int형으로 써놨는데, 보통 기하 문제들은 좌표값이 커서
왠만하면 안전하게 long long형으로 꼭 하시기를 바랍니다 ㅠㅠ
(괜히 대강 계산하고 얕봤다가 틀린경우가 있습니당 ㅠㅠ)
그래서 이를 통해서 접하는지에 대한 여부또한 ccw 알고리즘을 응용해서 알아볼수 있다
다음 대표적인 문제가 다음과 같다
사실 이문제는 union-find도 알아야 풀수는 있기는 한데, 우선은 딱히 문제가 없어서 가져왔습니다
문제를 요약하면, n개의 선분이 주어지고, 그 선분들이 교차하면 같은 그룹들로 묶고
그렇게 묶었을때 총 그룹의 갯수와, 가장 큰 그룹(선분의 개수가 가장 많은)의 선분갯수를 출력하는 문제이다
그래서, 선분이 교차하는지를 판별하고
만약 교차한다면, 그때 교차했을때의 두 집합의 조상(루트)이 다르다면, 합치고
같다면 합치지 않는다 라는 union -find를 이용해 접근해서 풀어보면 됩니다
C++
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <queue>
#include <map>
#include <iostream>
#include <string>
#include <math.h>
#include <set>
#include <list>
#include <climits>
#include <string.h>
#include <deque>
#include <functional>
#include <stack>
using namespace std;
typedef long long ll;
#define INF 1000000000
#define mod 1000000007
typedef pair<ll, ll> P;
typedef pair<pair<int, int>, int> PP;
typedef pair<int, pair<int, int>> PPP;
typedef pair<pair<ll, ll>, pair<ll, ll>> PPPP;
int gox[4] = { 0,1,-1,0 };
int goy[4] = { 1,0,0,-1 };
// 교차하거나 접하면, 선분이 겹치므로 그때 해당 선분을 union-find하면됨
// 선분을 저장할때, 정보가 4개필요하므로, pair4개로 ㄱㄱ
int parent[3005];
int Size[3005];
int n;
int find(int u) {
if (parent[u] == u) return u;
return parent[u] = find(parent[u]);
}
void uni(int u, int v) {
u = find(u);
v = find(v);
if (u == v) return;
if (Size[u] > Size[v]) {
Size[u] += Size[v];
Size[v] = 0;
parent[v] = u;
}
else {
Size[v] += Size[u];
Size[u] = 0;
parent[u] = v;
}
}
ll ccw(P A, P B, P C) {
int x1 = A.first, y1 = A.second, x2 = B.first, y2 = B.second, x3 = C.first, y3 = C.second;
return (x1*y2 + x2 * y3 + x3 * y1) - (x2*y1 + x3 * y2 + x1 * y3);
}
bool check(P A, P B, P C, P D) {
int x1 = A.first, y1 = A.second, x2 = B.first, y2 = B.second, x3 = C.first, y3 = C.second, x4 = D.first, y4 = D.second;
if (x1 == x2 && x2 == x3 && x3 == x4 & x4 == x1) { //x좌표 겹칠때(y좌표비교)
int maxy = max(y1, y2);
int miny = min(y3, y4);
if (maxy < miny) return false;
int maxy2 = max(y3, y4);
int miny2 = min(y1, y2);
if (maxy2 < miny2) return false;
}
else { //그외 나머지(기울기가 동일하다거나, y좌표가 겹친다거나)
int maxx = max(x1, x2);
int minx = min(x3, x4);
if (maxx < minx) return false;
int maxx2 = max(x3, x4);
int minx2 = min(x1, x2);
if (maxx2 < minx2) return false;
}
return true;
}
int main() {
vector<PPPP> v;
scanf("%d", &n);
for (int i = 0; i < n; i++) parent[i] = i;
for (int i = 0; i < n; i++) Size[i] = 1;
for (int i = 1; i <= n; i++) {
int x1, y1, x2, y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
v.push_back({ { x1,y1 }, {x2,y2} });
}
//각 선분에대해서 본인을 제외한 다른 선분끼리 ccw를 다해봐야 함(그리고 만약 인접하면 그때 union)하면될듯?
for (int i = 0; i < v.size(); i++) {
for (int j = 0; j < v.size(); j++) {
if (i == j)continue;
PPPP here = v[i];
PPPP next = v[j];
ll ccw1 = ccw(here.first, here.second, next.first);
ll ccw2 = ccw(here.first, here.second, next.second);
ll ccw3 = ccw(next.first, next.second, here.first);
ll ccw4 = ccw(next.first, next.second, here.second);
if (ccw1*ccw2 > 0 || ccw3 * ccw4 > 0) continue; //1차거르기
else { // 이제는 교차가 되는지 안되는지를 판단해야함, 만약 교차가 안되면 여기서도 거른다
if (check(here.first, here.second, next.first, next.second)) {
if (find(i) != find(j)) uni(i, j);
}
}
}
}
int cnt = 0;
int Max = 0;
for (int i = 0; i < n; i++) {
if (Size[i] != 0) cnt++;
Max = max(Max, Size[i]);
}
printf("%d\n%d\n", cnt, Max);
return 0;
}
by Java
package com.company;
import java.io.*;
import java.util.ArrayList;
import java.util.List;
import java.util.StringTokenizer;
import static java.lang.Long.max;
import static java.lang.Long.min;
public class Main {
static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
List<PP> v = new ArrayList<>();
int[] parent = new int[n];
int[] size = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
size[i] = 1;
}
for (int i = 0; i < n; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
long x1 = Long.parseLong(st.nextToken()), y1 = Long.parseLong(st.nextToken()), x2 = Long.parseLong(st.nextToken()), y2 = Long.parseLong(st.nextToken());
v.add(new PP(x1, y1, x2, y2));
}
for (int i = 0; i < v.size(); i++) {
for (int j = i + 1; j < v.size(); j++) {
PP here = v.get(i);
PP next = v.get(j);
long ccw1 = ccw(here.x1, here.y1, here.x2, here.y2, next.x1, next.y1);
long ccw2 = ccw(here.x1, here.y1, here.x2, here.y2, next.x2, next.y2);
long ccw3 = ccw(next.x1, next.y1, next.x2, next.y2, here.x1, here.y1);
long ccw4 = ccw(next.x1, next.y1, next.x2, next.y2, here.x2, here.y2);
if (ccw1 * ccw2 > 0 || ccw3 * ccw4 > 0) continue;
else {
if (ccw1 * ccw2 == 0 && ccw3 * ccw4 == 0 && !cross(here.x1, here.y1, here.x2, here.y2, next.x1, next.y1, next.x2, next.y2))
continue;
if (find(i, parent) != find(j, parent)) union(i, j, parent, size);
}
}
}
int cnt = 0, max = 0;
for (int i = 0; i < n; i++) {
if (size[i] != 0) {
cnt++;
if (max < size[i]) max = size[i];
}
}
bw.write(cnt + "\n" + max + "\n");
bw.flush();
bw.close();
}
private static void union(int u, int v, int[] parent, int[] Size) {
u = find(u, parent);
v = find(v, parent);
if (u == v) return;
if (Size[u] < Size[v]) {
Size[v] += Size[u];
Size[u] = 0;
parent[u] = v;
} else {
Size[u] += Size[v];
Size[v] = 0;
parent[v] = u;
}
}
private static int find(int u, int[] parent) {
if (u == parent[u]) return u;
return parent[u] = find(parent[u], parent);
}
private static boolean cross(long x1, long y1, long x2, long y2, long x3, long y3, long x4, long y4) {
if (x1 == x2 && x2 == x3 && x3 == x4) {
return !check(y1, y2, y3, y4);
} else {
return !check(x1, x2, x3, x4);
}
}
private static boolean check(long x1, long x2, long x3, long x4) {
long maxx = max(x1, x2);
long minx = min(x3, x4);
if (maxx < minx) return true;
maxx = max(x3, x4);
minx = min(x1, x2);
return maxx < minx;
}
private static long ccw(long x1, long y1, long x2, long y2, long x3, long y3) {
return (x1 * y2 + x2 * y3 + x3 * y1) - (x2 * y1 + x3 * y2 + x1 * y3);
}
}
class PP {
long x1, y1, x2, y2;
PP(long x1, long y1, long x2, long y2) {
this.x1 = x1;
this.y1 = y1;
this.x2 = x2;
this.y2 = y2;
}
}
class P {
long x;
long y;
P(long x, long y) {
this.x = x;
this.y = y;
}
}
선분에서 각 쌍의 x y좌표 들을 가지고 있어야 하기때문에(4개의 정보)
(구조체로 하는것이 일반적입니다ㅠㅠ) 전 pair를 너무 좋아해서.. 왠만하면 저런식으로 처리했습니다
양해 부탁드립니다(형변환을 해줘야 하는데, 위 코드는 해주지 않았습니다. 죄송합니다)
교차하는지에 대한 문제도 ccw 알고리즘을 이용해서 풀수 있다는 점입니다
궁금하신 사항은 댓글을 남겨주시면 감사하겠습니다^^
잘못 된점 이 있다면 댓글 남겨주시면 감사드리겠습니다

Leave a comment