CCW

CCW는 간략하게 CW와 CCW로 이루어진 말인것 같다

아무튼 CCW는 평면상의 임의의 세점이 있을때 그 점들간의 위치관계를 파악할수 있다는것이다

​경우는 3가지로 나뉘는데

1. 반시계 방향인 경우 : 이때는 ccw값이 양수(+)값이 나온다
2. 시계 방향인 경우 : 이때는 ccw값이 음수(-)가 나온다
3. 일직선인 경우 : 이때는 ccw값이 0이 나온다

​그림으로 간략하게 표현해 보면

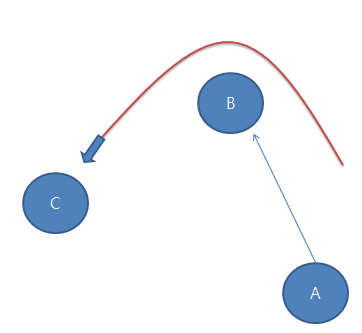
위의 그림은 반시계 방향을 이루는 경우이며

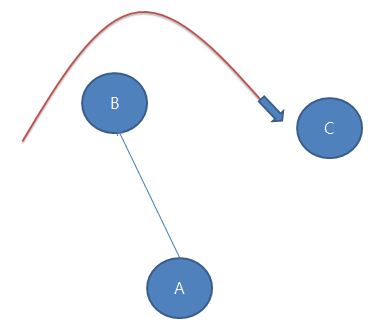
위의 그림은 시계방향을 이루는 경우이다
​나머지 한경우는 일직선이 될때의 경우이다.(따로 그림은 넣지는 않겠습니당) 기하와 벡터를 아예 모르는 경우에서 들으면 무슨말인지를 잘 모르지만, 간단하게 생각하면 옛날에 플래밍 법칙? 그거를 통해서 외워도 된다

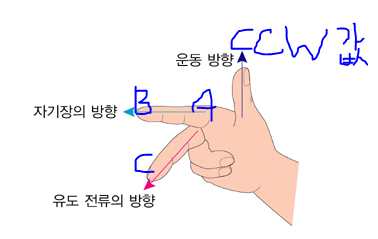
출처 : 그림 출처

여기서 중요한 사실 한가지가 있다면, 기준점이 되는 A와 B가 순서가 뒤바뀐다면, ccw값도 뒤바뀐다라는 점이다

즉, A->B, C를 판단하는것과, B->A , C를 판단하는 CCW알고리즘값은 다르다는 것이다. 일명 교환법칙이 성립하지 않는다라고 봐도 된다

그래서 ccw값을 구하는 공식은 행렬식을 이용한 공식이지만 복잡하니까, 쉽게 외울수 있는 방법을 가지고 왔다

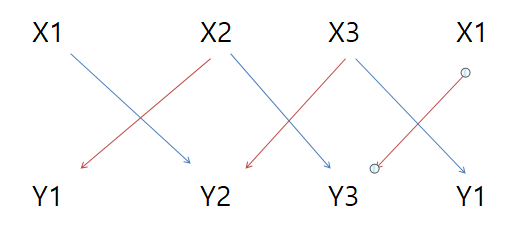
1. 파란색화살표끼리 곱하고, 빨간색화살표끼리 곱한다

2. 그다음 파란색화살표끼리 곱한 값들의 누적값과 빨간색화살표기리 곱한 누적값을 빼주면 된다.

​그래서 코드로 표현을 해보면

ll ccw(P A, P B, P C) {
    ll x1 = A.first, y1 = A.second, x2 = B.first, y2 = B.second, x3 = C.first, y3 = C.second;
    return (x1*y2 + x2 * y3 + x3 * y1) - (x2*y1 + x3 * y2 + x1 * y3);
}

• 저기서 P는 미리 헤더에 typedef pair<ll,ll> P; 라고 선언을 해주는 부분이다(x좌표와 y좌표를 표현해 주어야 하기때문!)

이를 통해서 CCW 알고리즘을 구현을 할수 있다

관련 문제 :

11758번: CCW

CCW 알고리즘을 통해서 여러 가지를 해볼수 있는데, 그중에서 대표적인 것이 다각형의 면적을 구하는 일이다

​여기서 CCW값은 단순히 방향성을 가지는 것 뿐만이 아니라 평행사변형의 넓이값을 의미하기도 한다(제가 잘못이해하고 있다면 댓글 부탁드립니당 ㅠㅠ)

​그래서 CCW값은 벡터의 외적을 통해 나오는 값(평행사변형 넓이)인데, 그 값을 반으로 나누면 삼각형의 면적을 구할수 있다는 얘기이다

​이 원리를 이용해서 다음과 같은 문제를 풀어볼 수 있다

문제 :

2166번: 다각형의 면적

접근 방법은 다음과 같다.

1.(0,0)의 점을 A라는 기준점을 잡는다.

1. B와 C를 현재 위치의 정점, 그리고 다음 위치의 정점으로 잡는다

2. 점 A,B,C를 통해 CCW를 돌린다.

3. CCW로 나온값이 음의 값인지 양의 값인지 체크를 한뒤, 음의 넓이를 누적해주는 변수와 양의 넓이를 누적해주는 변수에 저장한다

4. 마지막에 음의 넓이-양의 넓이, or 양의 넓이-음의 넓이 를 취한 다음 , 절대값을 씌운다

​즉, ccw를 통해서 평행사변형의 넓이를 구한다음 반으로 나누면 그 3개의 점을 통해서 이루는 삼각형의 면적을 구할수 있다는 것이다

그런데, 그 면적이 음인지 양인지에 따라 헷갈리는데, 음이면 시계방향이라는 뜻이고, 양이면 반시계방향으로 간다는 뜻일것이다

​근데 이문제는, 그냥 단순히 위의 두 경우를 전부다 양수화 시켜서 더해버리면, 분명히 중복하는 부분이 발생한다.

그래서 이걸 해결하는 방법은 단순하게도, 음의 넓이와 양의 넓이를 빼주면, 중복하는 부분이 사라지게 될것이라는 생각을 떠올려야 한다!

​그러므로 소스 코드는 다음과 같다

C++

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <queue>
#include <map>
#include <iostream>
#include <string>
#include <math.h>
#include <set>
#include <list>
#include <climits>
#include <string.h>
#include <deque>
#include <functional>
#include <stack>
using namespace std;
typedef long long ll;
#define INF 1000000000
#define mod 1000000007
typedef pair<double, double> P;
typedef pair<pair<int, int>, int> PP;
typedef pair<int, pair<int, int>> PPP;
typedef pair<pair<ll, ll>, pair<ll, ll>> PPPP;
int gox[4] = { 0,1,-1,0 };
int goy[4] = { 1,0,0,-1 };
int n;
double ccw(P A, P B, P C) {
    double x1 = A.first, y1 = A.second, x2 = B.first, y2 = B.second, x3 = C.first, y3 = C.second;
    return (x1*y2 + x2 * y3 + x3 * y1) - (x2*y1 + x3 * y2 + x1 * y3);
}

int main() {
    scanf("%d", &n);
    vector<P> v;
    v.push_back({ 0,0 }); // 미리 기준점 A를 넣고 시작
    for (int i = 1; i <= n; i++) {
        double x, y;
        scanf("%lf%lf", &x, &y);
        v.push_back({ x,y });
    }
    //0번점은 무조건 A, 1번지점 B,2번지점 C -> 2번지점 B,3번지점 C-> ... n번지점-> 1번지점
    double minustotal = 0;
    double plustotal = 0;
    for (int i = 1; i < v.size(); i++) {
        int here = i;
        int next = i + 1;
        if (here == v.size() - 1) next = 1; // 마지막 지점에 왔을때 n번지점, 1번지점의 경우도 체크해줘야함
        double c = ccw(v[0], v[here], v[next]);
        if (c > 0) {
            plustotal += (c / 2); // 삼각형의 면적구하기(양의 경우)
        }
        else {
            double temp = abs(c); // 음의 경우는 그냥 나눌수가 없기때문에, 절대값을 취해줘야한다!
            temp /= 2;
            minustotal += temp; // 음의 경우
        }
    }
    double total = minustotal - plustotal;
    if (total < 0) total = -total;
    printf("%.1lf\n", total);

    return 0;

}

Java

import java.io.*;
import java.util.ArrayList;
import static java.lang.Math.abs;
public class Main {
    static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        ArrayList<p> v = new ArrayList<>();
        for(int i=0;i<n;i++) {
            String[] input = br.readLine().split(" ");
            v.add(new p(Long.parseLong(input[0]),Long.parseLong(input[1])));
        }
        double plus = 0, minus = 0;
        for(int i=0;i<v.size();i++) {
            p a = v.get(i), b= v.get((i+1)%v.size());
            long temp = ccw(new p(0,0),a,b);
            if(temp > 0) {
                plus += ((double)temp/2);
            }
            else {
                minus += ((double)abs(temp)/2);
            }
        }
        System.out.println(String.format("%.1f",abs(plus-minus)));
    }
    private static long ccw(p a,p b,p c) {
        return (a.x*b.y+b.x*c.y+c.x*a.y) - (b.x*a.y+c.x*b.y+a.x*c.y);
    }
    private static class p {
        long x,y;
        private p(long x,long y) {
            this.x = x;
            this.y = y;
        }
    }
}

문제를 그냥 풀때 저렇게 변수 2개를 나누지 않고, 음이면 빼고, 양이면 더해서, 나중에 음수면 절대값을 취하는 형식으로 했는데 정답이 틀렸었다.

그래서 이런 문제로 틀리시는 분들은 저렇게 경우를 2개로 나눠서 처리하면 틀리지 않을것이기 때문에 참고하시면 좋을 것 같다

궁금하신 사항은 댓글을 남겨주시면 감사하겠습니다^^
잘못 된점 이 있다면 댓글 남겨주시면 감사드리겠습니다