ConvexHull
Updated:
Convex Hull (Monotone Chain 기법)
저도 컨벡스 헐을 배운지는 1주일도 안되서, 공부하고 기록의 차원이니 많이 이해해주셨으면 좋겠다.
우선 컨벡스 헐이라는건, 간단하게 2차원 평면에 n개의 점이 흩어져 있는데, 이 n개의 점중에 몇개를 선택해서 볼록 다각형을 만들때
그 다각형안에 나머지 모든 점을 포함시키게 하는 도형을 볼록 껍질 , 컨벡스헐이라고 한다
이 문제를 푸는데는 3가지 기법이 있다
-
Jarvis March 기법: 제일 작은(x,y)를 찾고, 그 다음으로 작은 좌표(극단점)를 찾고, 계속 반복을 한다(사실 잘모르겠다)
-
Graham Scan 기법: 각도 정렬 후에, 각도 순 탐색하면서 볼록 껍질 형성
-
Monotone Chain 기법: X축 정렬후, 위 껍질 탐색, 아래 껍질을 만들면 된다(Graham Scan 기법과 똑같이!!)
사실 1번과 2번을 안하고, 3번으로만 해서 방식은 잘 모르겠다 3번은 2번과 방법은 똑같은데, 과정을 2번한다고 보면 된다 과정은 다음과 같다
- 먼저 정렬을 한다(x좌표가 작은순서, 만약에 같다면 y좌표가 작은순서대로) -> 사실상 그냥 정렬을 하는거랑 똑같다고 보면된다
(2번은 하기조차 싫었던게 각도정렬을 해야 되서, 그게 너무 길어질거 같아서 안했음.. ㅠㅠ)
- 그다음 정렬이 되었으면, Stack 자료구조를 쓰면서 진행을 한다. (맨처음에는 첫번째 정점의 인덱스를 넣고, 두번째 정점의 인덱스를 넣는다)
- 이때 스택에서 먼저 나온 정점을 B 정점, 그다음 나온 정점을 A 정점이라 하자(즉 2개를 뽑았다는 의미), 이때 다음 정점을 C라고 한다면,
이때 CCW를 구한 값이 일관성이 있는 경우(+이든 -이든)에만, 스택에 넣어주고, 그렇지 않다면 스택하나를 pop한다
이게 무슨 소리인지 한번 써보도록 하겠습니다
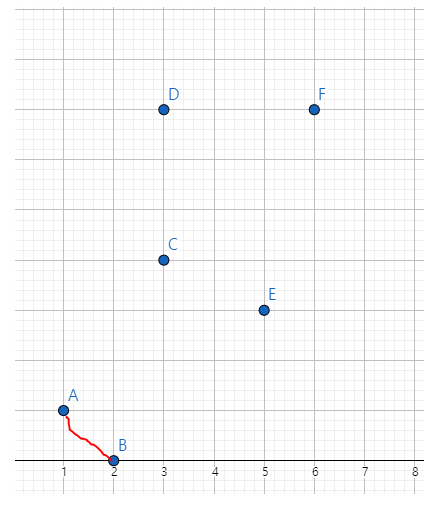
이런 입력값이 있을때, 무조건 처음좌표와 두번째 좌표는 넣고 시작을 해야 합니다
(즉 항상 스택의 사이즈는 2 이상이어야합니다!!!)
그다음 C 좌표를 봅니다
점 A,B 그리고 CCW한 값이 반시계방향 양수이므로, 우선은 넣어줍니다(우리는 CCW 양수만을 가지는 값을 선택한것입니다)
그러면 스택에는 A,B,C가 쌓일것입니다. 그렇게 다시 점 B와 C를 기준으로 다음 정점인 D를 봅니다
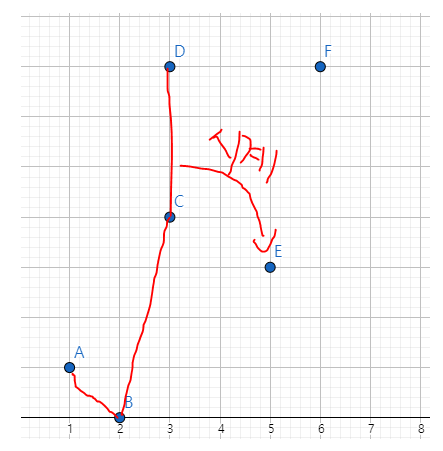
반시계방향이므로 D를 넣어줍니다. 이때 다시 선분CD를 기준으로 E를 볼때 시계방향이므로 유효하지 않습니다
다시 선분 BC를 기준으로 E를 봐도 마찬가지로 시계방향입니다
그러므로 스택에 있는 점 A,B,C에서 C를 빼주고, 다음정점인 E를 봅니다
이때 C가 빠지기 때문에 , 선분 BC는 유효하지 않게됩니다
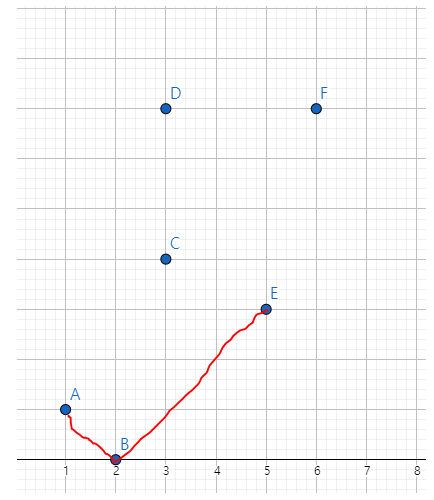
다시 점 A와 B를 기준으로 E를 보면 반시계방향이므로 , 올바르기 때문에 스택에 넣어줍니다
다음은 점 B와 점 E를 기준으로 F를 봅니다 또 반시계이므로, F도 넣어줍니다
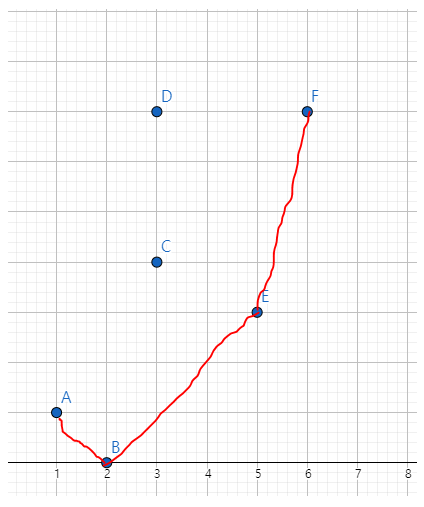
이제 끝점까지 갔기 때문에, 아래껍질이 형성 되었음을 알수 있습니다
다시 윗껍질을 형성하려면, 맨뒷점과 맨뒷점 전을 넣고, 이제는 뒤로 가면서 형성을 시키면됩니다
우리는 반시계방향으로 형성했기때문에, 윗껍질 또한 그런식으로 반복을 해주면 됩니다
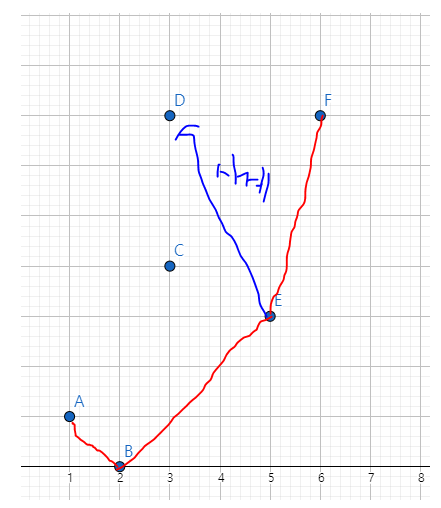
시계 방향이므로, 점F와 점E이므로, pop을 하면 점 E가 pop이 될것입니다. 즉 선분 EF는 의미가 없다는 뜻입니다.
그다음, 무조건 항상 스택 사이즈는 2이상 만들어야 하기때문에, 점 D를 넣어줍니다
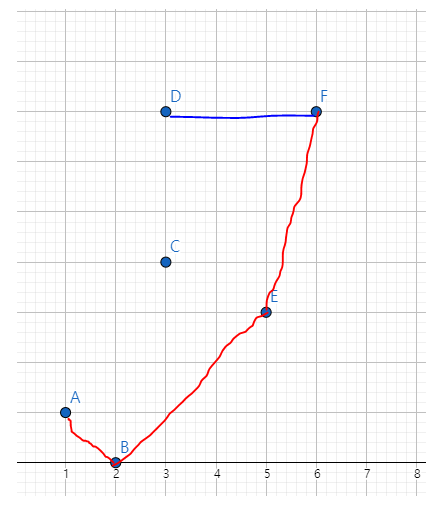
그러면 이상태가 될것입니다
다시 선분 FD를 기준으로 점 C를 보면 양방향이므로, 넣어줍니다
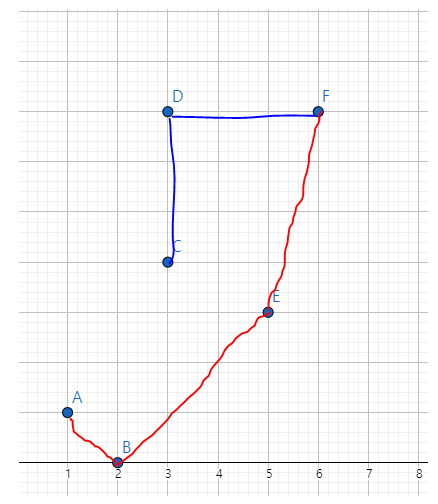
이제 똑같이 선분 DC를 기준으로 B를 보는데, 시계방향이므로 점C를 빼줍니다(포인터는 스택사이즈가 2미만일때만 이동합니다!!)
다시 선분FD를 기준으로 점 B를 보면, 반시계이므로 넣어줍니다 그러면 아래와 같이 될것입니다
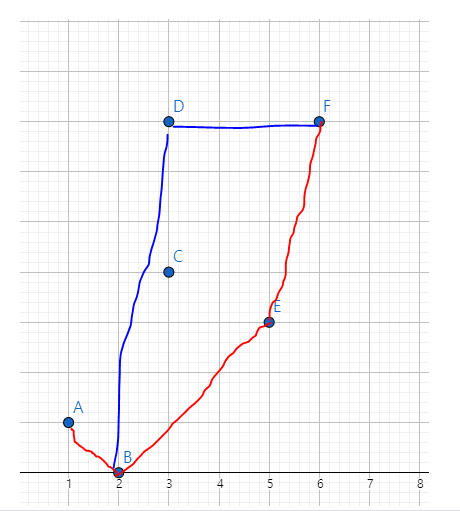
다시 선분 DB를 기준으로 점A를 CCW한 값은 시계방향이므로 스택에서 점B를 빼줍니다
그다음 다시 선분FD를 기준으로 점 A를 볼때, 반시계이므로 넣어주고, 더이상 A보다 작은 정점은 없기때문에 종료됩니다
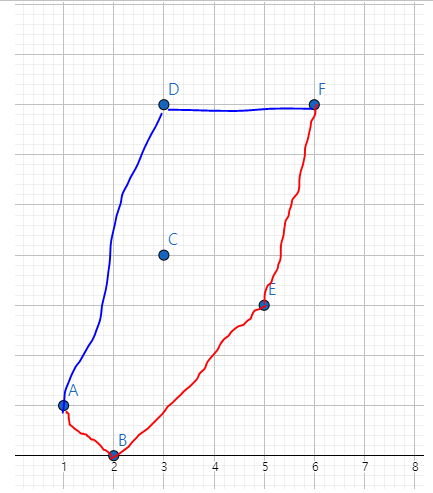
이런식으로 볼록 껍질이 형성됨을 알수 있습니다
요약을 하면
-
CCW한 값이 일관성있는 값(위의 예에서는 반시계방향)이 계속 나올때마다, 스택에 넣고, 인덱스포인터를 증가(아래껍질 형성),혹은 인덱스포인터를 감소시킵니다(윗껍질 형성)
-
만약 1번의 경우가 아닐시에는 스택에서 pop을 하고, 만약 스택사이즈가 2미만으로 될경우에는, 현 인덱스포인터를 넣어주고
인덱스 포인터를 증가(아래껍질)시키거나 감소(윗껍질)시켜줍니다.
- 스택사이즈가 2미만이 아니라면 인덱스포인터는 증가하거나 감소하지 않습니다!!
이 과정을 해준다면 우린 올바른 볼록껍질을 형성시킬수 있습니다
그래서 문제를 풀어보면
C++
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <queue>
#include <map>
#include <iostream>
#include <string>
#include <math.h>
#include <set>
#include <list>
#include <climits>
#include <string.h>
#include <deque>
#include <functional>
#include <stack>
using namespace std;
typedef long long ll;
#define INF 1000000000
#define mod 1000000007
typedef pair < ll, ll > P;
typedef pair<pair<int, int>, int> PP;
typedef pair<int, pair<int, int>> PPP;
typedef pair<pair<int, int>, pair<int, int>> PPPP;
int gox[4] = { 0,1,-1,0 };
int goy[4] = { 1,0,0,-1 };
int n;
vector<P> v;
map<ll, int> m;
stack<ll> st, en;
ll ccw(P A, P B, P C) {
ll x1 = A.first, y1 = A.second, x2 = B.first, y2 = B.second, x3 = C.first, y3 = C.second;
return (x1*y2 + x2 * y3 + x3 * y1) - (x2*y1 + x3 * y2 + x1 * y3);
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
ll x, y;
scanf("%lld%lld", &x, &y);
v.push_back({ x,y });
}
sort(v.begin(), v.end());
//graham scan방법으로 0~v.size()-1까지 돌린다(기준은 반시계방향, 시계방향이 나오면 걔를뺀다)
int ptr = 2;
st.push(0), st.push(1);
// 0부터 쭉 진행하기(반시계여야 값을 넣을수 있다-> 즉 ccw값이 양수일때)
while (ptr < v.size()) { // 아랫껍질 만들기
ll first = st.top();
st.pop();
ll second = st.top();
st.pop();
ll ccw1 = ccw(v[second], v[first], v[ptr]);
if (ccw1 > 0) {
st.push(second),st.push(first),st.push(ptr); //원상태로 만들고, ptr을 넣어줌
ptr++;
}
else {
st.push(second),st.push(first),st.pop(); //원상태로 만들고, pop해줌
if (st.size() == 1) { // 사이즈가 1이라면 항상 2를 만들어야함!!
st.push(ptr);
ptr++;
}
}
}
ptr = v.size() - 3;
en.push(v.size() - 1);
en.push(v.size() - 2);
while (ptr >= 0) {
ll first = en.top();
en.pop();
ll second = en.top();
en.pop();
ll ccw1 = ccw(v[second], v[first], v[ptr]);
if (ccw1 > 0) {
en.push(second),en.push(first),en.push(ptr);
ptr--;
}
else {
en.push(second),en.push(first),en.pop();
if (en.size() == 1) {
en.push(ptr);
ptr--;
}
}
}
while (!st.empty()) { //아랫껍질 갯수체크
if (m.count(st.top()) == 0) {
m[st.top()] = 1;
st.pop();
}
else st.pop();
}
while (!en.empty()) { //윗껍질 갯수체크
if (m.count(en.top()) == 0) {
m[en.top()] = 1;
en.pop();
}
else en.pop();
}
printf("%d\n", m.size());
return 0;
}
by Java
import java.io.*;
import java.util.*;
public class Main {
static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
ArrayList<p> v = new ArrayList<>();
for (int i = 1; i <= n; i++) {
st = new StringTokenizer(br.readLine());
long x = Long.parseLong(st.nextToken()), y = Long.parseLong(st.nextToken());
v.add(new p(x, y));
}
v.sort((a, b) -> {
if (a.x < b.x) return -1;
else if (a.x > b.x) return 1;
else {
if (a.y < b.y) return -1;
else if (a.y > b.y) return 1;
else return 0;
}
});
ArrayDeque<Integer> up = new ArrayDeque<>();
ArrayDeque<Integer> down = new ArrayDeque<>();
up.add(0);
up.add(1);
int ptr = 2;
while (ptr < v.size()) {
int second = up.peekLast();
up.pollLast();
int first = up.peekLast();
up.pollLast();
long ccw1 = ccw(v.get(first), v.get(second), v.get(ptr));
if (ccw1 > 0) {
up.add(first);
up.add(second);
up.add(ptr);
ptr++;
} else {
up.add(first);
if (up.size() == 1) {
up.add(ptr);
ptr++;
}
}
}
down.add(v.size() - 1);
down.add(v.size() - 2);
ptr = v.size() - 3;
while (ptr >= 0) {
int second = down.peekLast();
down.pollLast();
int first = down.peekLast();
down.pollLast();
long ccw1 = ccw(v.get(first), v.get(second), v.get(ptr));
if (ccw1 > 0) {
down.add(first);
down.add(second);
down.add(ptr);
ptr--;
} else {
down.add(first);
if (down.size() == 1) {
down.add(ptr);
ptr--;
}
}
}
HashMap<Integer, Integer> m = new HashMap<>();
int cnt = 0;
while (!up.isEmpty()) {
int here = up.peekLast();
up.pollLast();
if (m.get(here) == null) {
m.put(here, 1);
cnt++;
}
}
while (!down.isEmpty()) {
int here = down.peekLast();
down.pollLast();
if (m.get(here) == null) {
m.put(here, 1);
cnt++;
}
}
System.out.println(cnt);
}
private static long ccw(p a, p b, p c) {
return (a.x * b.y + b.x * c.y + c.x * a.y) - (b.x * a.y + c.x * b.y + a.x * c.y);
}
private static class p {
long x, y;
private p(long x, long y) {
this.x = x;
this.y = y;
}
}
}
문제를 잘 읽어보면, 이게 이제 볼록껍질 관련 문제에서 중요하다고 볼수 있는데,
다각형의 모든 점이 일직선을 이루는 경우가 없다 라는 경우가 있다.
이 말은 뭐냐면 선분을 이루는 직선 위에 다른 점이 포함될수 없다라는 말을 의미한다.
그렇기 때문에, 위 문제에서는 ccw가 0이되서 일직선을 이루는 경우는 체크를 해주지 않는다
하지만 다른 문제들을 접해보니, 볼록껍질을 이루는 직선위에 정점이 있는 경우도 체크를 해준다고 되어있다면
ccw는 0도 포함을 시켜줘야 한다. 이 문제는 좀더 고심해 보시면 될것같다
궁금하신 사항이 있으시면 댓글을 달아주시면 감사하겠습니다^^
잘못 된점 이 있다면 댓글 남겨주시면 감사드리겠습니다

Leave a comment